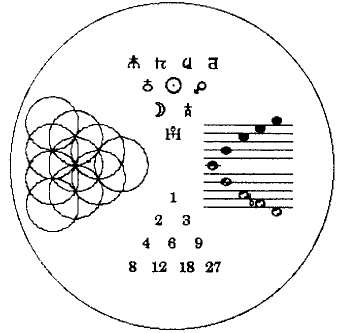

This "quadrivial compass" represents the intersection of Astrology, Music, Number, and Geometry. With an understanding of these four art/sciences, you can orient yourself in any unfamiliar field of knowledge. What are these four symbols?
What are the "liberal arts"? Nowadays, we usually define a liberal-arts education in the negative -- "impractical", the opposite of technical or professional training; rarely leads to a job, usually due for a cutback next year. It is a vague phrase used to lump together all the academic disciplines that we perceive as soft, subjective, in distinction from disciplines like law, business, the sciences, which are supposedly based on a hard, objective body of facts. In these money-dominated days, in which a college degree is seen merely as a ticket to a higher-paying job, we increasingly forget that a "liberal arts" education has always been meant, not to train one to perform specialized labor -- which is merely "vocational" teaching --, but to liberate the mind. The word comes from Latin liber, a "free man", one who is not a slave. Little wonder that, the more we become slaves to an omnipotent and all-pervading economic order, the less we remember the origin of the liberal arts as the curriculum of philosophers, priests, and magicians.
Originally the liberal arts were seven in number. They were divided into the three-fold Trivium of Grammar, Logic, and Rhetoric, and the four-fold Quadrivium of Arithmetic, Geometry, Music, and Astronomy. These words mean, respectively, a three-way and a four-way crossroads, implying that these paths of knowledge are fundamentally interconnected -- and, by extension, that all other paths can be found to intersect here, as well. The T. was the basis of elementary education (whence we probably get the word "trivial"): Grammar taught the craft of reading and writing; Logic, of careful reasoning; and Rhetoric, of effective communication. The Q. was the basis of advanced education: Arithmetic taught the science of number; Geometry, of form; Music, of sound (and of "harmony" in the most general sense of the word -- "number in motion", as it was often put); Astronomy, of time (of "form in motion"). Moreover, from the very beginning, whether openly acknowledged or carefully alluded to, each of the Quadrivial sciences was accompanied by its complementary metaphysical art. Each dealt not only with the outer structures, but also with the inner meanings of its discipline. Thus, Arithmetic included Arithmology, the understanding that numbers were not merely quantities, but also qualities (that "two", for instance, is also "duality, polarity"); Geometry included what is nowadays called Geomancy, the understanding (in, for example, the design of temples or cathedrals, or in the graphic arts) that the spirit and the emotions can be affected in particular ways by particular forms; Astronomy included Astrology, the divination of the meanings of cycles of time; and Music included not only the study of "practical theory", of nomenclature and technique (e.g. "this is a minor third", "this is the Mixolydian mode"), but also the study of "speculative theory", of the meanings and influences of tones and intervals and scales.
The choice of these particular disciplines was by no means arbitrary. Plato, who learned the arts of the Quadrivium from the school of Pythagoras (who, in turn, probably learned them from the priestly schools of Egypt or Babylon), exalted them in the Republic and the Laws as the essential education for the philosopher -- for the study of these art/sciences awakens the mind to the intrinsic order of the cosmos, freeing it from its bondage to mere "shadows on the cave wall". By studying the links and intersections among these disciplines, one learns to recognize analogies, patterns, correspondences, through which the archetypal Ideas that underlie and unite the cosmos manifest themselves in the world of time and space. Little wonder that, a thousand years after Pythagoras, as the Roman Empire was collapsing and the ancient libraries and academies were being burned and outlawed by religious fanatics, the seven liberal arts were the one essential seed of classical wisdom that was rescued and preserved by the monasteries through the so-called Dark Ages, to bloom in the Carolingian renaissance and yet again in the age of the cathedrals as the curriculum of the first universities. The Quadrivium flourished uninterruptedly in the philosophy, art, and science of medieval Islam; in fact, as interconnected sacred canons of measurement, of spatial orientation and architectural and artistic proportion, of musical scales and modes, and of calendric cycles, the four arts the West knew as the Quadrivium were also the basis of priestly and shamanic education and practice in ancient Egypt, Babylon, India, China, Meso-america -- indeed, in practically every pre-modern culture one can examine.
In the West, up through the Renaissance, the seven liberal arts retained an important role in education, and the influence of the Q. deeply pervaded the visual arts, architecture, music, and philosophy. Composers wrote musical works that were based on arithmetical patterns or, in at least one instance, on the geometry of the cathedral at whose dedication the work was performed (1). The proportions of cathedrals and palaces were in turn often borrowed from the "consonant" musical intervals. The astronomer (and astrologer) Kepler was led to his discovery of the mathematical laws of planetary motion by his investigation of the "music of the spheres" and his discovery that the five Platonic solids could be nested within the orbits of the known planets. Ficino's and Agrippa's magickal philosophies were based on the metaphysical arts of the Quadrivium. Such historical examples could be multiplied ad infinitum.
But they end rather suddenly in the 1600's, with the combined onslaught of the Christian "witch craze" -- which branded the metaphysical arts of the Q. as "satanic" and "occult" -- and the Scientific Revolution, which inaugurated a dogmatically materialistic view of the cosmos (originally, scholars such as Frances Yates (The Rosicrucian Enlightenment) and Carolyn Merchant (The Death of Nature) argue, as a protection against religious persecution, but which soon hardened into an ideology that fit conveniently with the increasing domination of society by commercial and economic interests). It was as if a heavy iron gate had abruptly slammed shut between the outer and the inner, between the left brain and the right, between the physical sciences and the metaphysical arts. After Descartes, Newton, and the Royal Academy, numerology was permanently factored out of arithmetic; numbers henceforth were allowed to signify only quantities, not qualities. Astronomy deliberately eclipsed astrology; time was decreed to be measurable only by the uniform ticks of the clock, not the variegated images of the zodiac. Geometry was circumscribed to exclude geomancy; shape and proportion were deprived of symbolism by engineer and artist both, as utilitarian and aesthete increasingly diverged from their once-shared perspective. Music was silenced from singing of any art but its own -- the scientists who commandeered its study of acoustics could only sneer at the "music of the spheres" and the "harmonies of heaven and earth", and the artists who inherited its practice of harmony and rhythm were eventually left with a mere technical argot of chord-names, scale-intervals, and key-signatures. Although the four Quadrivial sciences survived into the Age of Reason in the new materialist priestcraft of "physics", the four arts were largely abandoned (numerology), ridiculed (astrology), forgotten (geomancy), or isolated (music). The Crossroads was buried and soon forgotten, and the link it provided between the material and the spiritual order was severed. In the new world order, knowledge and truth could no longer be uncovered through the traditional reasoning of analogy and correspondence, but only through the revelation of the Bible or the proof of the test-tube -- that is, either religious faith or cause-and-effect materialism. Once the habit of "pattern"-thinking was replaced by "straight-line" thinking, knowledge lost its unity and interconnectedness, and began to fragment into ever smaller specialties, each with its own jargon, each dominated by its own elite of "experts".
Today, the process of specialization of knowledge has reached extreme proportions. We live in a Tower of Babble, bombarded by information and facts and expertise, little of which is expressed in a common language, even less of which is seen to interrelate or form a comprehensible overall pattern. Yet, on the other hand, we increasingly hear physicists, ecologists, and religious figures speak about holism, interconnectedness, the web of all being. We sense that this is true, that we and the cosmos do participate in an organic unity; but we have as yet found few ways to practice it, or even to understand it on a practical, meaningful level. Above all else, how do we teach it? Academics and educators are at long last beginning to show serious interest in "interdisciplinary" research and teaching, and the ability to reason analogically, to recognize patterns in common among seemingly diverse areas of knowledge and experience, is coming to be recognized increasingly (even, for example, by such a committed scientific materialist as Marvin Minsky, in a recent interview (2)) as a highly practical skill in a world where people must constantly adapt to ever more swiftly changing technologies, careers, and cultural and economic conditions. Perhaps it is time to re-connect ourselves with our past as well, and to excavate and rebuild the ancient pedagogy of the Crossroads -- but in a new way, appropriate to the environment of the Computer Age.
As if to prove the timelessness of the Q., I stumbled across it years before I knew of its name or its historical existence. My own specialty was music theory, and it was my interest in how and why scales, chords, and harmonies work as they do that led me to study vibrational ratios and harmonious proportions, and the physics of waves and cycles. From music's "cycles per second", it was not a very large step to "cycles per century", as it were -- the realm of astrology. In both, these systems of cycles are associated with analogous ideas and emotions. Soon, my work with tuning systems and calculating astrological charts by hand (I didn't have a computer; but it's really not that hard) cured me of a lifelong allergy to math. Suddenly, numbers were alive with meanings and associations. Rather than the disconnected sets of dry formulas I'd been made to memorize in school, I could hear and see mathematical patterns take shape. These patterns led me into geometry, and an interest in what we call geomancy and the Chinese call "feng shui": the intentional arrangement of space in architecture or landscape to create harmony or discord.
When you begin to follow a theme such as "cycles" or "proportions" -- or "resonance", "twelve", "symmetry", to name some others -- that runs through all four of these fields, you quickly find yourself learning about geometry and math, for example, while you thought you were simply studying music. Moreover, because the kinds of knowledge that the Q. teaches truly do intersect with nearly every other field of study, you find it far more easy and enjoyable to read and understand the underlying theories of texts on physics, electronics, ecology, computer science, philosophy, and many other technical specialties than it had ever been before. The Q. acts as a kind of "universal translating device", which -- because it represents all-pervasive patterns of order -- helps one to identify and build upon the most significant points of commonality between what one already knows and an unfamiliar new field or skill, and to penetrate the fog of jargon and terminology that so often obscures those points. It teaches you to recognize commonality and similarity, rather than the constant focus on distinctions and divisions and particularities, on learning as a linear march through a series of isolated compartments, that is enforced by conventional educational methods. In a larger sense, analogical understanding -- "that" is similar to (but not identical with) "this", "you" are similar to (but not identical with) "us" -- is an essential skill that seems to be largely missing today from a world increasingly dominated by religious separatism, factional warfare, and economic selfishness. One might even say that it is the intellect's counterpart to the emotion of compassion.
I think of the Q. as a kind of compass for navigating the Information Flood (a more accurate metaphor, it seems, than "superhighway"!). Just as you use a compass to orient you to the point on the earth where all lines of latitude and longitude unite, so you use the Q. to find the points where seemingly disparate areas of information converge. This is a twelve-fold compass, in which the arts of the Trivium are not added to the Q. as in the "seven liberal arts", but multiplied with it. Each Quadrivial discipline can be divided according to its "logic", its "grammar", and its "rhetoric". The logical branch is its scientific, "left-brain" side, the investigation into the laws by which it works; the rhetorical branch is its aesthetic, "right-brain" side, its expression of meaning and emotion, as well as its relationship to the spirit and soul; and the grammatical branch is the terminology and conventions it uses, a neutral middle ground which draws on both the logical and the rhetorical branches. For example, in Music, Grammar describes certain combinations of tones as "major triads", others as "minor triads". Logic observes that major triads are formed "upward", by frequency multiplication, with the smaller and more complex interval above the larger, simpler one, whereas the minor triad is formed "downward", by frequency division, exactly inverting the two intervals. Rhetoric uses the upward-tending major triad to express "yang" feelings like joy or courage, and the downward-tending minor triad to express "yin" feelings like sorrow or fear. I would go so far as to say that every field is usefully divisible into these three branches, and note that, by and large, the Logic and Grammar branches are nowadays given most of the educational and practical attention, whereas the Rhetorical branch is written off as arbitrary and random (because it is "non-quantifiable"), and ignored or left to individual whim. (If only architects considered the rhetoric of their geometry and not merely its logic, for example, we might have fewer harsh rectilinear surfaces dominating our landscapes and contributing to the anomie of modern life.)
Steven C. Rasmussen
March 28. 1996
Send e-mail to Steven C. Rasmussen at srasmus@oldenwilde.org. Tell me something about your own interests and background, too.
A website for teaching and learning music theory in innovative ways (currently under construction) is the first phase of a proposed Quadrivial website, called Liberal7Arts. (In The Goodly Spellbook, you can find a more complete version of the information on the 7 Modes that this prototype website demonstrates.)

(1) Guillaume Dufay, in the 15th century,
structured the motet "Nuper rosarum flores" according
to the architectural proportions of the Duomo in Florence, at
whose dedication the work was performed. Return
to text.
(2) In Mira Balaban et al., eds., Understanding
Music with Artificial Intelligence: Perspectives on Music Cognition,
1992 MIT Press, p. xi-xii. I cite this at length because Minsky
arrives at the same conclusion as me from the opposite end of
the philosophical spectrum:"So you think computer science
-- or at least AI -- needs other, richer kinds of descriptive
ideas and terms [than binary logic]? MM: Yes indeed. I want AI
researchers to appreciate that there is no one 'best' way to represent
knowledge. Each kind of problem requires appropriate types of
thinking and reasoning ... For example, logical methods are based
on using rigid rules of inference to make deductions. This works
well inside formal domains -- those artificial worlds that we
imagine for ourselves. But to cope with the unknowns and uncertainties
of reality, we must base our actions on experience -- and that
requires us to reason by analogy, because no two situations are
ever quite the same. In turn, this means that we have to be able
to recollect similar experiences and understand which differences
are relevant. But in the logical world, ideas like 'similar' and
'relevant' are alien because logic can only answer questions like
'what is this an instance of?' or 'what is this a generalization
of?' The trouble is that concepts like instance and generalization
apply only to ideas -- because no actual object or event can be
an instance of anything else. However, real things can be seen
as related -- at least in an observer's mind -- by apparent similarities
of structures, effects, or useful applications. Certainly this
is the case in music."Return to text.
Clockwise from top:
 Return to top of page.
Return to top of page.
![]() Return
to Meet Coven Oldenwilde's HP and HPS
Return
to Meet Coven Oldenwilde's HP and HPS
 Return to "Meet the Coven Members"
page.
Return to "Meet the Coven Members"
page.
![]() Return
to Coven Oldenwilde's home page.
Return
to Coven Oldenwilde's home page.
Latest update: 09 Mar. 2009
![]()